Let
 | (1) |
where
 | (2) |
so
 | (3) |
The total derivative of ![]() with respect to
with respect to ![]() is then
is then
 | (4) | ||
 | (5) |
In terms of ![]() and
and ![]() , (5) becomes
, (5) becomes
 | (6) | ||
 | (7) |
Along the real, or x-axis, 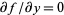 , so
, so
 | (8) |
Along the imaginary, or y-axis, 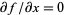 , so
, so
 | (9) |
If ![]() is complex differentiable, then the value of the derivative must be the same for a given
is complex differentiable, then the value of the derivative must be the same for a given ![]() , regardless of its orientation. Therefore, (8) must equal (9), which requires that
, regardless of its orientation. Therefore, (8) must equal (9), which requires that
 | (10) |
and
 | (11) |
These are known as the Cauchy-Riemann equations.
They lead to the conditions
| (12) | |||
| (13) |
The Cauchy-Riemann equations may be concisely written as
 | (14) | ||
 | (15) | ||
 | (16) | ||
| (17) |
where ![]() is the complex conjugate.
is the complex conjugate.
If ![]() , then the Cauchy-Riemann equations become
, then the Cauchy-Riemann equations become
| (18) | |||
| (19) |
(Abramowitz and Stegun 1972, p. 17).
If ![]() and
and ![]() satisfy the Cauchy-Riemann equations, they also satisfy Laplace’s equation in two dimensions, since
satisfy the Cauchy-Riemann equations, they also satisfy Laplace’s equation in two dimensions, since
 | (20) |
 | (21) |
By picking an arbitrary ![]() , solutions can be found which automatically satisfy the Cauchy-Riemann equations and Laplace’s equation. This fact is used to use conformal mappings to find solutions to physical problems involving scalar potentials such as fluid flow and electrostatics.
, solutions can be found which automatically satisfy the Cauchy-Riemann equations and Laplace’s equation. This fact is used to use conformal mappings to find solutions to physical problems involving scalar potentials such as fluid flow and electrostatics.