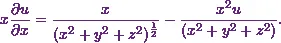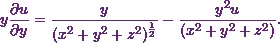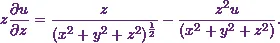First-Order Partial Derivative Of Functions With Three Variables

EXAMPLE 1

According to Stroud and Booth (2013)* “If 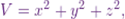V = x^2 + y^2 + z^2, express in its simplest form

\[x\frac{\partial V}{\partial x} + y\frac{\partial V}{\partial y} + z\frac{\partial V}{\partial z}.\]

SOLUTION

Here the given function is 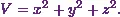V = x^2 + y^2 + z^2.

And, I have to find out the value of 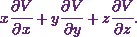$x\cfrac{\partial V}{\partial x} + y\cfrac{\partial V}{\partial y} + z\cfrac{\partial V}{\partial z}.$

So I’ll start with $\cfrac{\partial V}{\partial x}$ .

STEP 1

First of all, I’ll differentiate 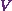partially with respect to to get

\[\frac{\partial V}{\partial x} = \frac{\partial }{\partial x}\left(x^2 + y^2 + z^2\right).\]

Thus I get

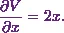
(1) $\begin{equation*} \frac{\partial V}{\partial x} = 2x. \end{equation*}$

Next, I’ll differentiate 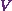partially with respect to to get

\[\frac{\partial V}{\partial y} = \frac{\partial }{\partial y}\left(x^2 + y^2 + z^2\right).\]

Therefore I get

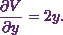
(2) $\begin{equation*} \frac{\partial V}{\partial y} = 2y. \end{equation*}$

Finally, I’ll differentiate 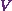partially with respect to to get

\[\frac{\partial V}{\partial z} = \frac{\partial }{\partial z}\left(x^2 + y^2 + z^2\right).\]

Thus I get

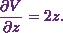
(3) $\begin{equation*} \frac{\partial V}{\partial z} = 2z. \end{equation*}$

So, now I’ll find out the value of 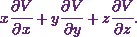$x\cfrac{\partial V}{\partial x} + y\cfrac{\partial V}{\partial y} + z\cfrac{\partial V}{\partial z}.$

STEP 2

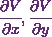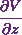For that, I’ll use the values of $\cfrac{\partial V}{\partial x}, \cfrac{\partial V}{\partial y}$ and $\cfrac{\partial V}{\partial z}$ from equations (1), (2) and (3) respectively.

Thus it will be

\[x\cfrac{\partial V}{\partial x} + y\cfrac{\partial V}{\partial y} + z\cfrac{\partial V}{\partial z}= x. 2x + y. 2y + z. 2z.\]

Therefore I get

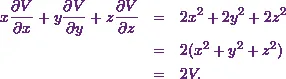
\begin{eqnarray*} x\frac{\partial V}{\partial x} + y\frac{\partial V}{\partial y} + z\frac{\partial V}{\partial z} &=& 2x^2+2y^2+2z^2\\ &=& 2(x^2+y^2 + z^2)\\ &=& 2V. \end{eqnarray*}

Hence I can conclude that this is the answer to this example.

Now I’ll go to the next example.

EXAMPLE 2

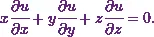According to Stroud and Booth (2013)* “If $u = \cfrac{x+y+z}{(x^2+y^2+z^2)^{\frac{1}{2}}}$ , show that $x \cfrac{\partial u}{\partial x}+ y \cfrac{\partial u}{\partial y} + z \cfrac{\partial u}{\partial z} = 0.$ ”

SOLUTION

In this example, the given function is $u = \cfrac{x+y+z}{(x^2+y^2+z^2)^{\frac{1}{2}}}$

And, I have to prove that 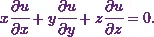$x\cfrac{\partial u}{\partial x} + y\cfrac{\partial u}{\partial y} + z\cfrac{\partial u}{\partial z} = 0.$

So I’ll start with 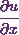$\cfrac{\partial u}{\partial x}$ .

STEP 1

First of all, I’ll differentiate partially with respect to to get

\[\frac{\partial u}{\partial x} = \frac{\partial }{\partial x}\left(\cfrac{x+y+z}{(x^2+y^2+z^2)^{\frac{1}{2}}}\right)\\= \frac{(x^2+y^2+z^2)^{\frac{1}{2}}.1-\frac{1}{2}(x^2+y^2+z^2)^{-\frac{1}{2}}(2x)(x+y+z)}{x^2+y^2+z^2}.\]

Therefore I get

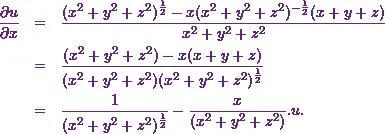
\begin{eqnarray*} \frac{\partial u}{\partial x} &=& \frac{(x^2+y^2+z^2)^{\frac{1}{2}}-x(x^2+y^2+z^2)^{-\frac{1}{2}}(x+y+z)}{x^2+y^2+z^2}\\ &=& \frac{(x^2+y^2+z^2)-x(x+y+z)}{(x^2+y^2+z^2)(x^2+y^2+z^2)^{\frac{1}{2}}}\\ &=& \frac{1}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{x}{(x^2+y^2+z^2)}.u. \end{eqnarray*}

Thus I can say 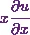$x\cfrac{\partial u}{\partial x}$ will be

(4) $\begin{equation*} x\frac{\partial u}{\partial x} = \frac{x}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{x^2u}{(x^2+y^2+z^2)}. \end{equation*}$

In the same way I can also get the value of 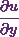$\cfrac{\partial u}{\partial y}$ .

Thus 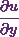$\cfrac{\partial u}{\partial y}$ will be

\[\frac{\partial u}{\partial y}= \frac{1}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{y}{(x^2+y^2+z^2)}.u.\]

Therefore I can say 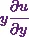$y\cfrac{\partial u}{\partial y}$ will be

(5) $\begin{equation*} y\frac{\partial u}{\partial y} = \frac{y}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{y^2u}{(x^2+y^2+z^2)}. \end{equation*}$

Similarly I can also get the value of 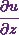$\cfrac{\partial u}{\partial z}$ .

Thus 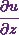$\cfrac{\partial u}{\partial z}$ will be

\[\frac{\partial u}{\partial z}= \frac{1}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{z}{(x^2+y^2+z^2)}.u.\]

Therefore I can say 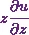$z\cfrac{\partial u}{\partial z}$ will be

(6) $\begin{equation*} z\frac{\partial u}{\partial z} = \frac{z}{(x^2+y^2+z^2)^{\frac{1}{2}}}-\frac{z^2u}{(x^2+y^2+z^2)}. \end{equation*}$

So, now I’ll find out the value of 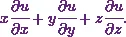$x\cfrac{\partial u}{\partial x} + y\cfrac{\partial u}{\partial y} + z\cfrac{\partial u}{\partial z}.$

STEP 2

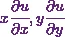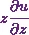For that, I’ll use the values of $x\cfrac{\partial u}{\partial x}, y\cfrac{\partial u}{\partial y}$ and $z\cfrac{\partial u}{\partial z}$ from equations (4), (5) and (6) respectively.

Thus it will be

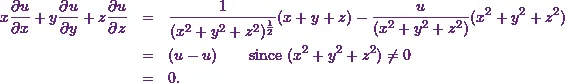
\begin{eqnarray*} x\frac{\partial u}{\partial x} + y\frac{\partial u}{\partial y} + z\frac{\partial u}{\partial z} &=& \frac{1}{(x^2+y^2+z^2)^{\frac{1}{2}}}(x+y+z)-\frac{u}{(x^2+y^2+z^2)}(x^2+y^2+z^2)\\ &=& (u-u)~~~~~~\text{since}~(x^2+y^2+z^2)\neq0\\ &=& 0. \end{eqnarray*}

Hence I can conclude that I have proved 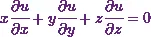$x\cfrac{\partial u}{\partial x} + y\cfrac{\partial u}{\partial y} + z\cfrac{\partial u}{\partial z} = 0$ .

This is the answer to this example.