Suppose  is a product of two functions
is a product of two functions 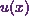 and
and 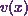 . This means
. This means 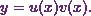
Now my task is to differentiate  , that is, to get the value of
, that is, to get the value of 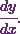 Since
Since  is a product of two functions, I’ll use the product rule of differentiation to get the value of
is a product of two functions, I’ll use the product rule of differentiation to get the value of 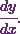 Thus
Thus 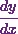 will be
will be
![\[\frac{dy}{dx} = u(x)\frac{dv}{dx}+ v(x)\frac{du}{dx}.\]](https://appassets.softecksblog.in/engineering_mathematics/assets/em2/9_files/image007.webp)
Next, I will give some example .
EXAMPLE
According to Stroud and Booth (2013)* “Differentiate 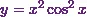 .”
.”
SOLUTION
STEP 1
Here the given function is: 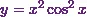 .
.
Now  is a product of two functions
is a product of two functions 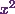 and
and 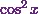 .
.
In order to differentiate  with respect to
with respect to  , I’ll use the product rule of differentiation.
, I’ll use the product rule of differentiation.
Thus it will be
![\[\frac{dy}{dx} = x^2\frac{d}{dx} (\cos^2 x) + \cos^2 x \frac{d}{dx}(x^2).\]](https://appassets.softecksblog.in/engineering_mathematics/assets/em2/9_files/image012.webp)
So this means
![\[\frac{dy}{dx} = x^2 (2 \cos x)\frac{d}{dx}(\cos x) + \cos^2 x (2x).\]](https://appassets.softecksblog.in/engineering_mathematics/assets/em2/9_files/image013.webp)
Now this gives
![\[\frac{dy}{dx} = x^2 (2 \cos x)(-\sin x) + 2x \cos^2 x.\]](https://appassets.softecksblog.in/engineering_mathematics/assets/em2/9_files/image014.webp)
At the end I’ll simplify it to get the value of 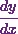 as
as
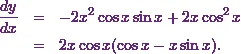
Hence I can conclude that this is the answer to the given example.