Divergence Of A Vector Function – Engineering Mathematics

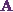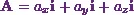Suppose I have a vector $\textbf{A}$ such as $\textbf{A} = a_x \textbf{i} + a_y \textbf{i} + a_z\textbf{i}$ .

Now the divergence of this vector 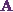$\textbf{A}$ will be

\[\text{div}~\textbf{A} = \nabla . \textbf{A} = \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z}.\]

So if I use the technique for first-order partial differentiation of functions with three variables, I will get the divergence of the vector.

If interested, you can read more about the other posts in vector analysis like directional derivative, the gradient of a scalar field, unit normal vector, unit tangent vector, curl of any vector and so on.

Now I’ll give some examples on the divergence of a vector function.

EXAMPLE

According to Kreyszig (2005)*, “Find the divergence of the following vector function: $[e^{2x}\cos 2y,~~~e^{2x}\sin 2y,~~~5e^{2z}]$ .”

SOLUTION

Now here the given vector is $[e^{2x}\cos 2y,~~~e^{2x}\sin 2y,~~~5e^{2z}]$ .

First of all, I’ll give it a name, say, 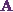$\textbf{A}$ .

So, in vector form, it will be

\[\textbf{A} = e^{2x}\cos 2y\textbf{i}+e^{2x}\sin 2y\textbf{j}+5e^{2z}\textbf{k}.\]

As per the the formula for the divergence of any vector, divergence of 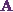$\textbf{A}$ will be

\[\text{div}\textbf{A}= \nabla . \textbf{A} = \frac{\partial}{\partial x}(e^{2x}\cos 2y) + \frac{\partial}{\partial y} (e^{2x}\sin 2y) + \frac{\partial}{\partial z} (5e^{2z}).\]

Thus it will be

\[\nabla . \textbf{A} = \cos 2y\frac{\partial}{\partial x}(e^{2x}) + e^{2x}\frac{\partial}{\partial y} (\sin 2y) + 5\frac{\partial}{\partial z} (e^{2z}).\]

So this means

\[\nabla . \textbf{A} = \cos 2y (2.e^{2x}) + e^{2x} (2\cos 2y) + 5 (2. e^{2z}).\]

Now I’ll simplify it to get

\[\nabla . \textbf{A} = 2e^{2x}\cos 2y + 2 e^{2x} \cos 2y + 10 e^{2z}\]

which means

\[\nabla . \textbf{A} = 4e^{2x}\cos 2y + 10 e^{2z}.\]

Hence I can conclude that this is the solution to the given example.