Posted inbasic

The Area Under A Parametric Curve

 

Suppose x = f(\theta) and y = g(\theta) are the parametric equations of a curve. Then the area bounded by the curve, the x-axis and the ordinates \theta = a and \theta = b will be

\[\text{Area} = \int_a^b y dx.\]

Now I’ll solve some examples of that.

EXAMPLE 1

According to Stroud and Booth (2013)*, “Determine the area of one arch of the cycloid x = \theta - \sin \theta, y = 1 - \cos \theta, i.e. find the area of the plane figure bounded by the curve and the x-axis between \theta = 0 and \theta = 2 \pi.”

SOLUTION

Now here the given parametric equations of the cycloid are

\[x = \theta - \sin \theta, y = 1 - \cos \theta.\]

And I have to find out the area of the plane figure bounded by the curve and the x-axis between \theta = 0 and \theta = 2 \pi. So I’ll start with the formula

\[\text{Area} = \int_0^{2\pi} y dx.\]
STEP 1

First of all, I’ll find out the value of dx in terms of d\theta. As I know the value of x is

\[x = \theta - \sin \theta.\]

Next, I’ll differentiate x with respect to \theta to get

\[\frac{dx}{d\theta} = 1 - \cos \theta.\]

So that gives

\[dx = (1 - \cos \theta) d\theta.\]

Therefore the area bounded by the curve and the x-axis between \theta = 0 and \theta = 2 \pi is

\[\text{Area} = \int_0^{2\pi} (1 - \cos \theta) (1 - \cos \theta) d\theta.\]

Then I’ll simplify it to get

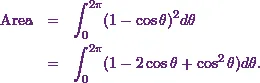
\begin{eqnarray*}\text{Area} &=& \int_0^{2\pi} (1 - \cos \theta)^2 d\theta\\ &=& \int_0^{2\pi} (1 - 2\cos \theta + \cos^2 \theta) d\theta.\end{eqnarray*}

As per the standard formulas in trigonometry,

\[\cos 2 \theta = 2 \cos^2 \theta - 1.\]

And that means,

\[\cos^2 \theta = \frac{1}{2}\left(1 + \cos 2 \theta \right).\]

So the area will be

\[\text{Area} = \int_0^{2\pi} \left[ 1 + \frac{1}{2}\left(1 + \cos 2 \theta \right) - 2 \cos \theta \right]d\theta.\]

Next, I’ll integrate it.

STEP 2

And for that, I’ll use the standard formulas in integration. Thus it will be

\[\text{Area} = \left[ \theta + \frac{1}{2}\left(\theta + \frac{\sin 2 \theta}{2}\right) - 2 \sin \theta \right]_0^{2\pi}.\]

Now I’ll substitute the limits to get

\begin{eqnarray*}\text{Area} &=& \left[ 2\pi + \frac{1}{2}\left(2\pi + \frac{\sin 4\pi}{2}\right) - 2 \sin 2\pi \right]\\&& - \left[ 0 + \frac{1}{2}\left(0 + \frac{\sin 0}{2}\right) - 2 \sin 0 \right].\end{eqnarray*}

As I know, \sin 0 = \sin 2 \pi = \sin 4 \pi = 0. So I’ll put these values in the equation of the area and simplify it to get

\begin{eqnarray*}\text{Area} &=& \left[ 2\pi + \frac{1}{2}\left(2\pi +0\right) - 2 (0) \right]\\&& - \left[ \frac{1}{2}\left( \frac{0}{2}\right) - 0 \right]\\ &=& [2 \pi + \pi - 0]-[0]\\ &=& 3 \pi .\end{eqnarray*}

Therefore the area bounded by the curve and the x-axis between \theta = 0 and \theta = 2 \pi is 3 \pi.

Hence I can conclude that this is the answer to the given example.

Now I’ll give another example.

EXAMPLE 2

According to Stroud and Booth (2013)*, “The parametric equations of a curve are y = 2 \sin \cfrac{\pi}{10}t, x = 2 + 2t - 2 \cos \cfrac{\pi}{10} t. Find the area under the curve between t = 0 and t = 10.”

SOLUTION

Now here the parametric equations of a curve are y = 2 \sin \cfrac{\pi}{10}t, x = 2 + 2t - 2 \cos \cfrac{\pi}{10} t. And I have to find the area under the curve between t = 0 and t = 10. So I’ll start with the formula

\[\text{Area} = \int_0^{10} y dx.\]
STEP 1

First of all, I’ll find out the value of dx in terms of d t. As I know the value of x is

\[x = 2 + 2t - 2 \cos \cfrac{\pi}{10} t.\]

Next, I’ll differentiate x with respect to t to get

\[\frac{dx}{dt} = 0+ 2 + 2 \sin \left(\frac{\pi}{10}t\right) \times \frac{\pi}{10}.\]

So that gives

\[dx = \left\{2 + \frac{\pi}{5}\sin \cfrac{\pi}{10}t \right\}dt.\]

Therefore the area under the curve between t = 0 and t = 10 is

\[\text{Area} = \int_0^{10} 2 \sin \cfrac{\pi}{10}t \left\{2 + \frac{\pi}{5}\sin \cfrac{\pi}{10}t \right\}dt.\]

Then I’ll simplify it to get

\[\text{Area} = \int_0^{10} \left\{4\sin \cfrac{\pi}{10}t + \frac{2\pi}{5}\sin^2 \cfrac{\pi}{10}t \right\}dt.\]

As per the standard formulas in trigonometry,

\[\cos 2 \theta = 1 -2 \sin^2 \theta.\]

And that means,

\[\sin^2 \theta = \frac{1}{2}\left(1 - \cos 2 \theta \right).\]

So the area will be

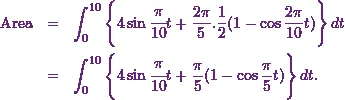
\begin{eqnarray*} \text{Area} &=& \int_0^{10} \left\{4\sin \cfrac{\pi}{10}t + \frac{2\pi}{5}.\frac{1}{2}(1 - \cos\frac{2 \pi}{10}t)\right\}dt\\&=& \int_0^{10} \left\{4\sin \cfrac{\pi}{10}t + \frac{\pi}{5}(1 - \cos \frac{\pi}{5}t)\right\}dt.\end{eqnarray*}

Next, I’ll integrate it.

STEP 2

And for that, I’ll use the standard formulas in integration. Thus it will be

\[\text{Area} = \left[- 4 \cos \cfrac{\pi}{10}t \times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(t - \sin \frac{\pi}{5}t \times \frac{1}{\pi/5})\right]_0^{10}.\]

Now I’ll substitute the limits to get

\begin{eqnarray*} \text{Area} &=& \left[- 4 \cos \cfrac{\pi}{10}.10\times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(10 - \sin \frac{\pi}{5}.10 \times \frac{1}{\pi/5})\right]\\ && - \left[- 4 \cos \cfrac{\pi}{10}.0 \times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(0 - \sin \frac{\pi}{5}.0 \times \frac{1}{\pi/5})\right]\end{eqnarray*}

Then I’ll simplify it to get

\begin{eqnarray*} \text{Area} &=& \left[- \frac{40}{\pi} \cos \pi + 2 \pi - \sin 2 \pi\right]\\ && - \left[- \frac{40}{\pi} \cos 0 + \frac{\pi}{5}( - \sin 0 \times \frac{1}{\pi/5})\right].\end{eqnarray*}

As I know \cos 0 = 1, \cos \pi = -1 and \sin 0 = \sin 2 \pi = 0. So I’ll put these values in the equation of the area. And that gives

\[\text{Area} = \left[- \frac{40}{\pi} (-1) + 2 \pi - 0\right]- \left[- \frac{40}{\pi} (1) + \frac{\pi}{5}( - 0 . \frac{1}{\pi/5})\right].\]

Now I’ll simplify it to get

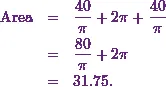
\begin{eqnarray*} \text{Area} &=& \frac{40}{\pi} + 2 \pi + \frac{40}{\pi} \\ &=& \frac{80}{\pi} + 2 \pi \\ &=& 31.75. \end{eqnarray*}

Thus the area under the curve between t = 0 and t = 10 is 31.75.